Education • All: 1.1 Terminology

DEFINITIONS AND TERMINOLOGY

1. Ordinary Differential Equation = y" + y ' + y = 0

2. Partial Differential Equation = 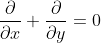$\frac{\partial }{\partial x}+\frac{\partial }{\partial y}=0$

We want our ordinary differential equation in normal form as follows:

y" + y' + y = 0

y" = -(y' + y)

$\frac{d^{2}y}{dx^{2}} = f(y ,\frac{dy}{dx})$

LINEAR DIFFERENTIAL EQUATION

y" + y' + y = 0 --> Linear

y" + y' + y² = 0 ---> Non linear

y" + y' + cosy = 0 --> Non linear
y" + yy' --> Non linear

Note: Functions that use "y" directly, (ie. cosy), will make the equation be non-linear.

Some definitions!

1. Explicit = Functions that can be written in the calculator, ie. y = sin(x) + x²

2. Implicit = As a relation, not as a function, ie. x² + y² = 25

3. Singular = y' + y = 5 --> y = 5

4. Trivial = y' + y = 0 --> y = 0 (Not the same as singular, y must be 0)

5. General = dy/dx = eˣ --> ʃdy = ʃeˣ dx --> y = eˣ + C

6. Particular = initial conditions are given, ie. (0,2) y = eˣ + 1

EXAMPLES

By using the definitions, describe the following:

① $\frac{d^{3}y}{dx^{3}} - (\frac{dy}{dx})^{4}+y=0$

=> Ordinary, Non-linear

② $\frac{d^{2}u}{dr^{2}} + 3 \frac{du}{dr}+u=\cos (r+u)$

=> Ordinary, Non-linear

③ $\frac{d^{2}R}{dt^{2}} = \frac{K}{R^{2}}$

=> Ordinary, Non-linear

4. Is the following linear in the dependent variable v? u?

④

$\large \\udv\;+\;(v+uv-ue^{u})du=0\\udv=-(v+uv-ue^{u})du\\\frac{dv}{du}+(\frac{v}{u}-ve^{u})=0\\v = linear!$

⑤

$\large \\udv\;+\;(v+uv-ue^{u})du=0\\\\\frac{u}{v+uv-ue^{u}}+\frac{du}{dv}=0\\\\u=Non-linear!$

Pages